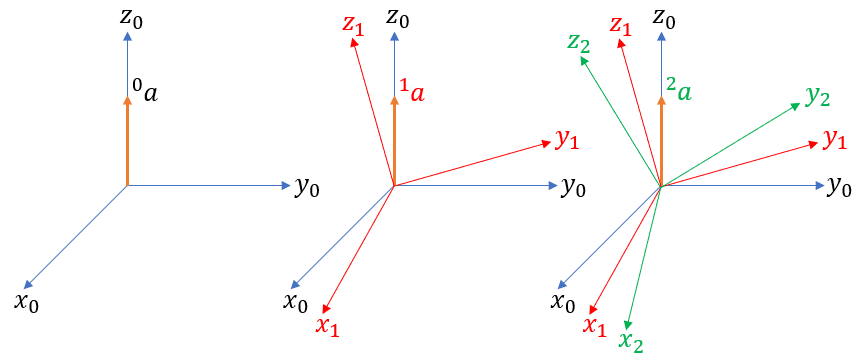
Rotate Frame
각도 계산을 위한 몇가지 가정을 하겠습니다.
- global(0) frame의 관찰자가 볼 때 0a는 크기와 방향이 바뀌지 않는다.
- 0 frame에서 회전을 시작하여 n 번째 관측된 좌표계를 n frame이라하고, 충분히 짧은 시간 간격으로 관측한다.
- k frame에서 k+1 frame으로 회전할 때 x, y, z 축 기준으로 회전각을 측정할 수 있다.
- 충분히 짧은 시간 관측하므로, 측정된 회전각은 small angle approximation을 적용해도 될만큼 충분히 작다.
k frame에서 k+1 frame으로 회전할 때, x축으로 dϕ, y축으로 dθ, **z축으로 dψ**만큼 회전했다면 각 축을 기준으로 회전 쿼터니언은 아래와 같습니다.
q(x^,dϕ)q(y^,dθ)q(z^,dψ)=[sin2dϕ00cos2dϕ]T=[0sin2dθ0cos2dθ]T=[00sin2dψcos2dψ]T≈[2dϕ001]T≈[02dθ01]T≈[002dψ1]T(dϕ→0)(dθ→0)(dψ→0)
회전각이 큰 경우 회전 순서에 따라 결과가 달라지지만 충분히 작은 경우 회전 순서에 따른 결과가 크게 다르지 않습니다.
q(a1,θ1)q(a2,θ2)=q(a2,θ2)q(a1,θ1)
q(a1,dθ1)q(a2,dθ2)≈q(a2,dθ2)q(a1,dθ1)dθ→0
k frame에서 k+1 frame으로 회전할 때, 충분히 작은 각도 변화라고 가정했으므로 임의로 Z-Y-X 순으로 회전했다고 가정하여 qk+1k를 구하면 아래와 같습니다.
qk+1kqk+1k≈≈q(z^,dψ)q(y^,dθ)q(x^,dϕ)[2dϕ2dθ2dψ1]T
각 구간별 회전각 측정을 통해 0 frame에서 n frame이 되는 회전 쿼터니언을 구할 수 있습니다.
qn0=q10q21⋯qnn−1
qn0=[qxqyqzqw]T
small angle approximation에 의해 시간이 흐름에 따라 누적 오차가 증가합니다.
Euler angles
x축, y축, z축 각 축을 기준으로하는 회전 행렬은 아래와 같습니다.
rot(X,ϕ)rot(Y,θ)rot(Z,ψ)===10000cosϕsinϕ00−sinϕcosϕ00001cosθ0−sinθ00100sinθ0cosθ00001cosψsinψ00−sinψcosψ0000100001
Euler angles에는 proper Euler angles과 Tait-Bryan angles 두 그룹이 있습니다. 각 그룹은 6개의 회전 순서를 갖습니다.
AHRS 구성을 위해 Z-Y-X 순서를 사용하는 Tait-Bryan angle을 사용하겠습니다.
일반적으로 Z축을 Yaw, Y축을 Pitch, X축을 Roll이라고 부릅니다. 방향은 아래 그림과 같이 설정하겠습니다.
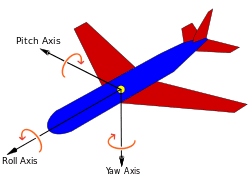
Z-Y-X Euler angle에 의한 회전행렬은 아래와 같습니다.
0a=rot(Z,ψ)rot(Y,θ)rot(X,ϕ)na=Rn0=cosθcosψcosθsinψ−sinθ0R12R22sinϕcosθ0R13R23cosϕcosθ00001na
R12R13R22R23=sinϕsinθcosψ−cosϕsinψ=cosϕsinθcosψ+sinϕsinψ=sinϕsinθsinψ+cosϕcosψ=cosϕsinθsinψ−sinϕcosψ
Quaternions and Euler angles
회전각의 측정을 통해 쿼터니언 회전 행렬의 경우 값을 알 수 있는 행렬입니다. 쿼터니언 회전 행렬과 Euler angle(Z-Y-X) 회전 행렬을 비교하면 AHRS 를 통해 구하고자 하는 Attitude와 Heading을 구할 수 있습니다.
1−2(qy2+qz2)2(qxqy+qzqw)2(qxqz−qyqw)02(qxqy−qzqw)1−2(qx2+qz2)2(qyqz+qxqw)02(qxqz+qyqw)2(qyqz−qxqw)1−2(qx2+qy2)00001=cosθcosψcosθsinψ−sinθ0R12R22sinϕcosθ0R13R23cosϕcosθ00001
ϕθψ=atan2(2(qyqz+qxqw),1−2(qx2+qy2))asin(2(qyqw−qxqz))atan2(2(qxqy+qzqw),1−2(qy2+qz2))
